241. In a strained body, three principal stresses at a point are denoted by σ₁, σ₂ and σ₃ such that σ₁ > σ₂ > σ₃. If σ₀ denoted yield stress, then according to the maximum
shear stress theory σ₁ - σ₃ = σ₀
242. The shear centre of a section is defined as that point through which load must be applied to produce zero twisting moment on the section
243
244.If the area under the shear curve for a beam between the two points X₁ and X₂ is 'k', then the difference between the moments at the two points X₁ and X₂ will
be equal to k
245. The ratio of the flexural strengths of two beams of square cross-section, the first beam being placed with its top and bottom sides horizontally and the second beam being placed with one diagonal horizontally, is √2
246. A short column of external diameter D₁ and internal diameter D₂ carries an
external load W. For no-tension condition, the eccentricity will be
247. A three hinged semicircular arch of radius R carries a uniformly distributed load ' W' per unit run over the whole span. The horizontal thrust is WR/2
248. A simply supported rectangular beam of span 'L' and depth 'd' carries a central load 'W'. The ratio of maximum deflection to maximum bending stress is
L² / 6 Ed
249. Consider the following statements regarding a beam of uniform cross section
simply supported at its ends and carrying a concentrated load at one of its third points:
1) The bending moment under the load will be maximum.
2) The slope at the nearer support will be maximum.
250. If the diameter of a shaft subjected to torque alone is doubled, then the horse
power P can be increased to 8P
251. If the strain energy absorbed in a cantilever beam in bending under its own
weight is 'K' times greater than the strain energy absorbed in an identical simply
supported beam in bending under its own weight, then the magnitude of 4K' is
6
252. A thin cylindrical shell of internal diameter 'D' and thickness T is subjected
to internal pressure 'p' The change in diameter is given by
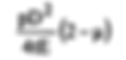
253
254. Consider the following statements: A simply supported beam is subjected to a couple somewhere in the span. It would produce
1. a rectangular SF diagram
2. both +ve and -ve BMs which are maximum at the point of application of the couple
255. A rectangular timber beam is cut out of a cylindrical log of diameter 'D' The depth of the strongest timber beam will be
256. A beam of length 10 m carries a udl of 20 kN/m over its entire length and rests on two simple supports. In order that the maximum BM produced in the beam is the least possible, the supports must be placed from the ends at a distance of
2.07 m
257. A beam of square cross- section (B x B) is used as a beam with one diagonal
horizontal. The location of the maximum shear stress from the neutral axis will be at a distance of B/4√2
258. An overhang beam of uniform EI is loaded as shown in Fig.
The deflection at the free end will be
259. A cast iron pipe of 1m diameter is required to withstand a 200 m head of
water. If he limiting tensile stress of the pipe material is 20 MPa, then the
thickness of the pipe will be 50 mm
260. For the flitched beams shown in Fig.10.46(1) and 10.46 (II), for the same value
of maximum bending stress in timber,
MR₁>MR₂