1. The number of independent equations to be satisfied for static equilibrium of a
plane structure is 3
2. If there are m unknown member forces, r unknown reaction components and j
number of joints, then the degree of static indeterminacy of a pin-jointed plane frame is given by (m + r - 2j)
3.Number of unknown internal forces in each member of a rigid jointed plane
frame is 3
4.Degree of static indeterminacy of a rigid jointed plane frame having 15 members, 3 reaction components and 14 joints is 6
5.Degree of kinematic indeterminacy of a pin-jointed plane frame is given by
2j - r
6.Independent displacement components at each joint of a rigid-jointed plane frame are-two linear movements and one rotation
7.If in a pin-jointed plane frame (m + r) >2j, then the frame is - stable and statically indeterminate
8.A pin-jointed plane frame is unstable if (m + r) < 2j
9.A rigid-jointed plane frame is stable and statically determinate if (3m + r) = 3j
10. Which of the beams shown in Fig. 12.1 is unstable ?
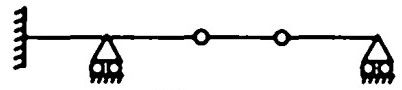
11 Degree of kinematic indeterminacy of the beam shown in Fig. 12.2 is
10
12. The rigid-jointed frame shown in Fig. 12.3 is
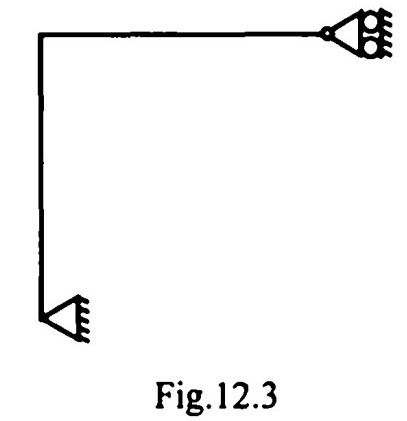
stable and statically determinate
13.The degree of kinematic indeterminacy of the pin-joined frame shown in Fig. 12.4 is
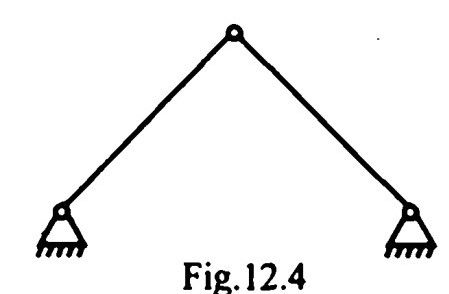
2
14. The number of independent equations to be satisfied for static equilibrium in a
space structure is 6
15. The degree of static indeterminacy of a pin-jointed space frame is given by
m + r - 3j
16. The degree of static indeterminacy of a rigid-jointed space frame is
6m + r - 6j
17. The degree of kinematic indeterminacy of a pin-jointed space frame is
3j-r
18. The number of independent displacement components at each joint of a rigid-jointed space frame is 6
19.If in a rigid-jointed space frame, (6m + r) < 6j, then the frame is -unstable
20.The principle of virtual work can be applied to elastic system by considering
the virtual work of-internal as well as external forces